IDENTIDAD

una identidad es la igualdad entre 2 expresiones que matematicamente se escribben distinto pero es lo mismo:

ejemplo

X^{2 + 2X + 1= (X+1)}2

cuando en una identidad se vuelven involucradas las funciones trigonometricas esta se consideran identidades trigonometricas:

ejemplo

Sen²Ө+Cos²Ө=1

(0,86)²+(0,5)²

^0,75+0,25=1

IDENTIDADES FUNDAMENTALES 

las identidades fundamentales son aquellas que se determinan de las funciones trigonométricas, estas identidades nos sirven para transformar otras identidades y comprobarlas.

DEMOSTRACION DE UNA IDENTIDAD

el metodo de demostracion de una identidad consiste en demostrar de una identidad consiste en demostrar que un miembro es igual al otro para ello se sujiere los siguientes pasos .

1)transformar el miembro mas complejo de la igualdad en  el miembro mas simple haciendo uso de la identidad,

2)si es posible expresar las funciones trigonometricas que aparezcan en la igualdad en terminos de las funciones "SEN y COS".

3)realizar las operaciones algebraicas para simplificar la expresion.

LEY DEL SENO 

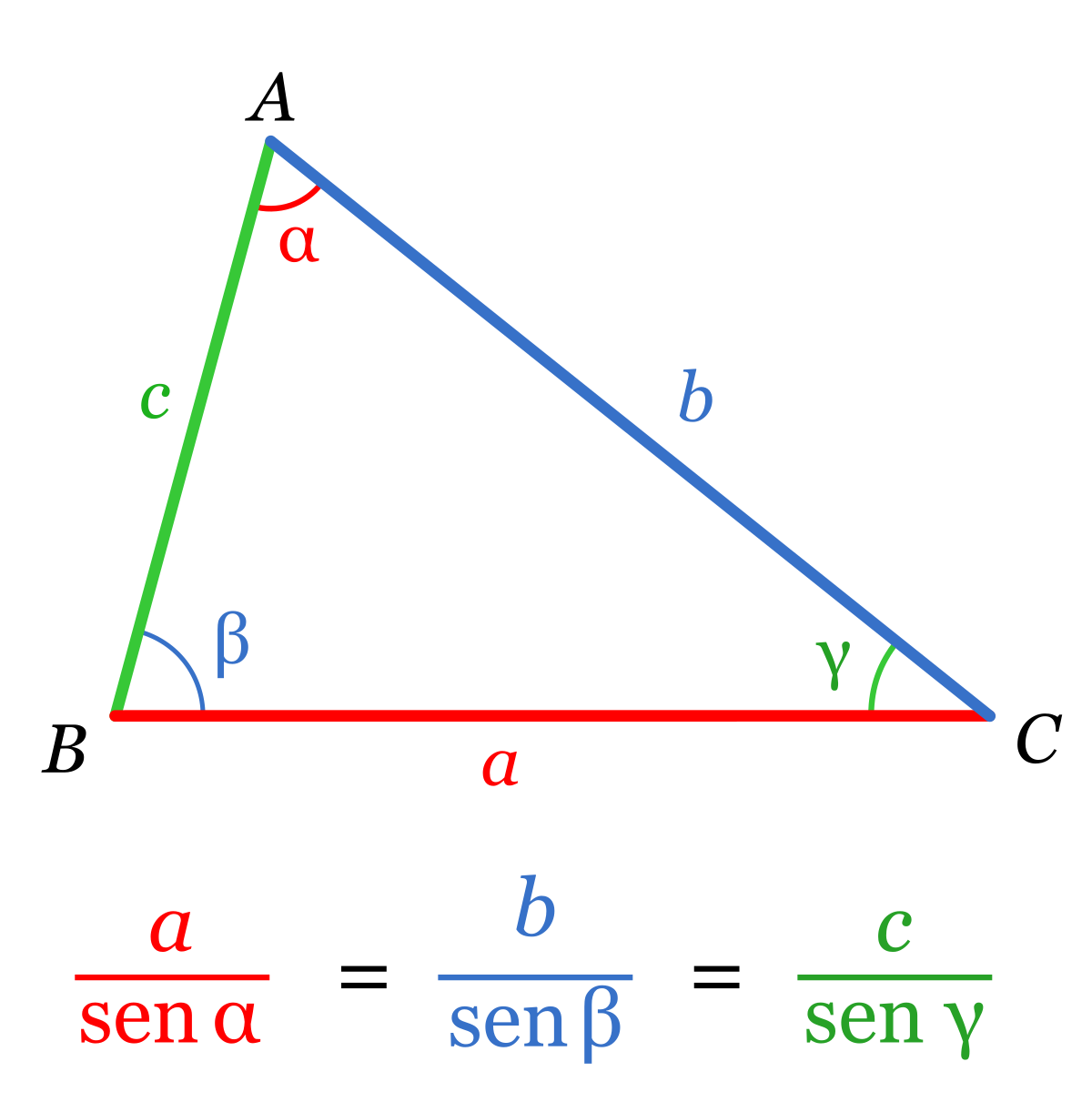
Es la relacion entre los lados y angulos de triangulos no rectangulos (obliculo) simplemente, establece la relacion de la longitud de un lado de un triangulo al seno del angulo opuesto a ese opuesto a ese lado es igual para todos los lados y angulos en un triangulo dado.

En triangulo A Bc es un triangulo obliculo con lados a,b y c , entonces  se determina en el ejemplo:

LEY DEL COSENO

La ley de los cosenos es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse.

La ley de los cosenos establece:

  c 2 = a 2 + b 2 – 2 ab cos C .

Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos.

La ley de los cosenos también puede establecerse como

b 2 = a 2 + c 2 – 2 ac cos B or

 a 2 = b 2 + c 2 – 2 bc cos A .