FUNCIÓN  CIRCULAR 

una función circular matemática de dos sentidos en una variedad diferenciable ${\displaystyle M}$, es una función escalar ${\displaystyle M\to {\mathbb {R} }}$ cuyos puntos críticos son un enlace, es decir, una unión desjunta de componentes conexos, cada uno siendo homeotermos al círculo ${\displaystyle S^{1}}$.

Por ejemplo, sea  el toro. Sea  entonces el mapeo  dado por

${\displaystyle X(\theta ,\phi )=((2+\cos \theta )\cos \phi ,(2+\cos \theta )\sin \phi ,\sin \theta )\,}$

CIRCUNFERENCIA UNITARIA 

El estudio de las funciones trigonométricas requiere al analizi de su comportamiento en la identificación de su dominio y sus rangos para realizar dicho analizi se considera la circunferencia de radio y centrada como en el origen el plano cartesiano.

La circunferencia unitaria es aquella que tiene como centro el origen del plano cartesiano y del radio de la unidad. 

En la figura anterior se muestra la circunferencia unitaria que contiene al punto p(x,y). Al aplicar el teorema de pitagora se obtiene que para todo punto p(x,y) se cumple que: _X^2  +_y^{2= 1} 

ANGULO DE REFERENCIA 

  Si θ es un angulo cuadrantal, se llama angulo de referencia θ, al angulo agudo que forma el lado final del angulo θ con uno de los semiejes del eje x. 

      Cuadrante I:  El ángulo dado y el ángulo de referencia son el mismo ángulo.

        α = θ

Cuadrante II:  α = π – θ (radianes)

        α  = 180°– θ (grados)

 Cuadrante III: α  =  θ – π (radianes)

         α = θ – 180° (grados)

      

   Cuadrante IV:  α = 2 π – θ (radianes)

   α = 360° – θ   (grados)

dos)

      

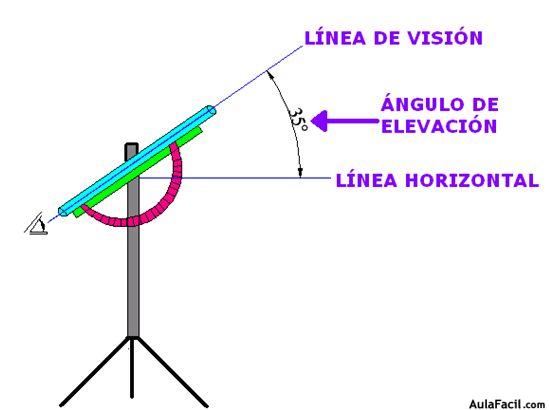
ANGULOS DE ELEVACION Y DEPRESICION

Son ángulos formados por dos líneas imaginarias llamadas: línea visual o línea de visión y la línea horizontal.

En estos casos, el observador se encuentra por debajo del objeto observado o bien, se encuentra por encima de dicho objeto.

Para estas mediciones se utilizan sencillos aparatos que colocados sobre un trípode ( 3 puntos determinan un solo plano) el simple giro realizado de la mirilla sobre el punto a observar nos señala los grados girados respecto a la horizontal:

TRIGONOMETRIA ANALITICA

en las expersiones algebraicas se utilizan variables y constantes cuyos valores pertenecen al conjunto de los numeros reales. en esta unidad se aplicaran algunos procedimientos utilizados en algebras a expresiones que imbolucran funciones trigonometricas o en los valores de esta pertenecen al conjunto de los numeros reales.

MULTIPLICACION DE EXPRESIONES TRIGONOMETRICA 

Para multiplicar expresiones que involucren funciones trigonométricas se aplica las propiedades de la potencia y la propiedades distributiva de la multiplicación 

PROPIEDADES DISTRIBUTIVA 

-4 (2+3)= -8-12=120

6(5-6)= (6 X 5)- (6 X4) = 30-24=6

FACTORIZACION

FACTORIZACION DE EXPRESIONES CON FUNCIÓN TRIGONOMÉTRICAS: Es posibles factorizar expresiones que involucran las funciones trigonométricas mediante lo mismo métodos de la factorizacion del polinomios

FACTOR COMÚN : En este caso es necesario identificar el factor que aparezca en todos los términos y aplicar la propiedad distributivas 

X (Y+Z)

X- Y +X Z

X (Y +Z)

FACTOR COMÚN POR AGRUPACIÓN 

En este casos se separan las expresiones en 2 o mas partes iguales (igual cantidad de terminos). en cada una de ella se identifica el factor común y se aplica la propiedad distributivas 

EJEMPLOS

1._(3cos³_{X + 6cos}²_{x) + (2cosx +4)}

(3.1 _cos²_{x+ 3.2 cos}²_{x)+ (2.1 cosx + 22)}

_3cos²_{x(1cosx + 2) + 2(1cosx +2)}

_{(1cosx +2) (3cos}²_x +2)

DIFERENCIAS DE CUADRADO

la diferencias de los cuadrados de 2 expresiones que involucran funciones trigonométricas es igual a la suma por la diferencia de las expresiones

TRINOMIO AL CUADRADO PERFECTO 

Un trinomio cuadrado perfecto, por brevedad TCP, es un polinomio de tres términos (también llamado trinomio) que resulta de elevar al cuadrado un binomio.

Todo trinomio de la forma:
${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}\,\!}$
es un trinomio cuadrado perfecto ya que
${\displaystyle (a+b)^{2}=(a+b)(a+b)=\,\!}$
${\displaystyle a^{2}+ab+ab+b^{2}=a^{2}+2ab+b^{2}\,\!}$

Siendo la regla: Cualquier suma de binomios al cuadrado es igual al cuadrado del primer término, más el doble del primer por el segundo término, más el cuadrado del segundo término. De lo anterior resulta que un trinomio será cuadrado perfecto siempre que se cumplan las siguientes condiciones:

1. El polinomio pueda ser ordenado en potencias descendentes de una variable.
2. Dos de los términos son cuadrados perfectos.
3. El otro término es el doble producto de las raíces cuadradas de los demás.
4. El primer y tercer término deben de tener el mismo signo