La linea recta

En geometría euclidiana, la recta o la línea recta es una línea que se extiende en una misma dirección por tanto tiene una sola dimensión y contiene un número infinito de puntos. Dicha recta también se puede describir como una sucesión continua de puntos extendidos en una sola dirección.

Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición solo es posible a partir de la descripción de las características de otros elementos similares. Un ejemplo de las dificultades de la definición de la recta a partir de puntos es la llamada paradoja de Zenón de la dicotomía que ilustraba la desaparición de la recta al dividirla en puntos porque luego no había un concepto para ensamblar dicha recta a partir de puntos ya que la unión de dos puntos es un punto. Las rectas se suelen denominar con una letra minúscula.

La Circuferencia

La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro.

Distíngase del círculo, que es el lugar geométrico de los puntos contenidos en el interior de dicha circunferencia, o sea, la circunferencia es el perímetro del círculo. Los puntos de la circunferencia están a una distancia igual al radio del centro del círculo, mientras los demás puntos del círculo están a menor distancia que el radio.

Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales, o los focos coinciden; o bien fuera una elipse cuyas directrices están en el infinito. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono regular de infinitos lados, cuya apotema coincide con su radio.

La elipse

Distíngase del círculo, que es el lugar geométrico de los puntos contenidos en el interior de dicha circunferencia, o sea, la circunferencia es el perímetro del círculo. Los puntos de la circunferencia están a una distancia igual al radio del centro del círculo, mientras los demás puntos del círculo están a menor distancia que el radio.

Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales, o los focos coinciden; o bien fuera una elipse cuyas directrices están en el infinito. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono regular de infinitos lados, cuya apotema coincide con su radio.

La parabola

Una parábola es una curva en la que los puntos están a la misma distancia de:

• un punto fijo (el foco), y
• una línea fija (la directriz

Estos son los nombres más importantes:

• la directriz y el foco (están explicados arriba)
• el eje de simetría(pasa por el foco, perpendicular a la directriz)
• el vértice(donde la parábola hace el giro más fuerte) está a medio camino entre el foco y la directriz.

Ecuaciones Si pones la parábola en coordenadas cartesianas(gráfico x-y) con: el vértice en el origen "O" y el eje de simetría en el eje x, entonces la curva queda definida por la ecuación: y2 = 4ax Ejemplo: ¿dónde está el foco de la ecuación y2=5x ? Si ponemos y2 = 5x en la forma y2 = 4ax, tenemos que y2 = 4 (5/4) x, así que a = 5/4, y el foco de y2=5x es: F = (a,0) = (5/4,0)

La hiperbole

La hipérbola es el lugar geométrico de los puntos de un plano cuya diferencia de distancias (d₁ y d₂) a dos puntos fijos llamados focos (F₁ y F₂) es constante.

El valor de esa constante es la distancia entre los vértices V₁ y V₂ de la hipérbola (2a).

La hipérbola también se puede definir como una cónica, siendo la intersección del cono con un plano que no pase por su vértice y que forme un ángulo con el eje del cono menor que el ángulo que forma con el eje generatriz g del cono.

Elementos de la hiperbole

Los elementos de la hiperboles son:

• Focos: son los dos puntos fijos (F₁ y F₂).
• Radio vector: es la distancia R de un punto de la hipérbola (P) a cualquiera de los focos.
• Eje focal: es el eje de simetría E que une a los dos focos. También se llama eje transverso.
• Eje no transverso: es la mediatriz T del eje focal.
• Centro: es el punto medio O de los dos focos. También se puede definir como la intersección del eje focal y el transverso.
• Vértices: son los dos puntos de intersección del eje focal con la hipérbola (V₁ y V₂).

• Distancia focal: es la distancia 2c entre focos. También se denota como F₁F₂.
• Eje real: es es la distancia 2a entre vértices.
• Eje imaginario: es la distancia 2b de los puntos B₁ y B₂. Los puntos B₁ y B₂ se generan como vemos en las relaciones entre semiejes.Así pues, existe una relación entre los semiejes y la distancia focal
• 

IDENTIDAD

una identidad es la igualdad entre 2 expresiones que matematicamente se escribben distinto pero es lo mismo:

ejemplo

X^{2 + 2X + 1= (X+1)}2

cuando en una identidad se vuelven involucradas las funciones trigonometricas esta se consideran identidades trigonometricas:

ejemplo

Sen²Ө+Cos²Ө=1

(0,86)²+(0,5)²

^0,75+0,25=1

IDENTIDADES FUNDAMENTALES 

las identidades fundamentales son aquellas que se determinan de las funciones trigonométricas, estas identidades nos sirven para transformar otras identidades y comprobarlas.

DEMOSTRACION DE UNA IDENTIDAD

el metodo de demostracion de una identidad consiste en demostrar de una identidad consiste en demostrar que un miembro es igual al otro para ello se sujiere los siguientes pasos .

1)transformar el miembro mas complejo de la igualdad en  el miembro mas simple haciendo uso de la identidad,

2)si es posible expresar las funciones trigonometricas que aparezcan en la igualdad en terminos de las funciones "SEN y COS".

3)realizar las operaciones algebraicas para simplificar la expresion.

LEY DEL SENO 

Es la relacion entre los lados y angulos de triangulos no rectangulos (obliculo) simplemente, establece la relacion de la longitud de un lado de un triangulo al seno del angulo opuesto a ese opuesto a ese lado es igual para todos los lados y angulos en un triangulo dado.

En triangulo A Bc es un triangulo obliculo con lados a,b y c , entonces  se determina en el ejemplo:

LEY DEL COSENO

La ley de los cosenos es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse.

La ley de los cosenos establece:

  c 2 = a 2 + b 2 – 2 ab cos C .

Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos.

La ley de los cosenos también puede establecerse como

b 2 = a 2 + c 2 – 2 ac cos B or

 a 2 = b 2 + c 2 – 2 bc cos A .

FUNCIÓN  CIRCULAR 

una función circular matemática de dos sentidos en una variedad diferenciable ${\displaystyle M}$, es una función escalar ${\displaystyle M\to {\mathbb {R} }}$ cuyos puntos críticos son un enlace, es decir, una unión desjunta de componentes conexos, cada uno siendo homeotermos al círculo ${\displaystyle S^{1}}$.

Por ejemplo, sea  el toro. Sea  entonces el mapeo  dado por

${\displaystyle X(\theta ,\phi )=((2+\cos \theta )\cos \phi ,(2+\cos \theta )\sin \phi ,\sin \theta )\,}$

CIRCUNFERENCIA UNITARIA 

El estudio de las funciones trigonométricas requiere al analizi de su comportamiento en la identificación de su dominio y sus rangos para realizar dicho analizi se considera la circunferencia de radio y centrada como en el origen el plano cartesiano.

La circunferencia unitaria es aquella que tiene como centro el origen del plano cartesiano y del radio de la unidad. 

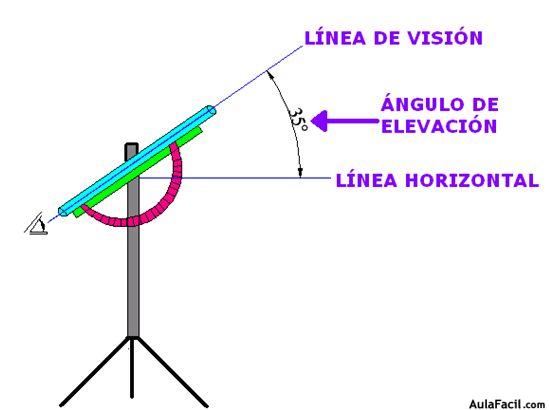
En la figura anterior se muestra la circunferencia unitaria que contiene al punto p(x,y). Al aplicar el teorema de pitagora se obtiene que para todo punto p(x,y) se cumple que: _X^2  +_y^{2= 1} 

ANGULO DE REFERENCIA 

  Si θ es un angulo cuadrantal, se llama angulo de referencia θ, al angulo agudo que forma el lado final del angulo θ con uno de los semiejes del eje x. 

      Cuadrante I:  El ángulo dado y el ángulo de referencia son el mismo ángulo.

        α = θ

Cuadrante II:  α = π – θ (radianes)

        α  = 180°– θ (grados)

 Cuadrante III: α  =  θ – π (radianes)

         α = θ – 180° (grados)

      

   Cuadrante IV:  α = 2 π – θ (radianes)

   α = 360° – θ   (grados)

dos)

      

ANGULOS DE ELEVACION Y DEPRESICION

Son ángulos formados por dos líneas imaginarias llamadas: línea visual o línea de visión y la línea horizontal.

En estos casos, el observador se encuentra por debajo del objeto observado o bien, se encuentra por encima de dicho objeto.

Para estas mediciones se utilizan sencillos aparatos que colocados sobre un trípode ( 3 puntos determinan un solo plano) el simple giro realizado de la mirilla sobre el punto a observar nos señala los grados girados respecto a la horizontal:

TRIGONOMETRIA ANALITICA

en las expersiones algebraicas se utilizan variables y constantes cuyos valores pertenecen al conjunto de los numeros reales. en esta unidad se aplicaran algunos procedimientos utilizados en algebras a expresiones que imbolucran funciones trigonometricas o en los valores de esta pertenecen al conjunto de los numeros reales.

MULTIPLICACION DE EXPRESIONES TRIGONOMETRICA 

Para multiplicar expresiones que involucren funciones trigonométricas se aplica las propiedades de la potencia y la propiedades distributiva de la multiplicación 

PROPIEDADES DISTRIBUTIVA 

-4 (2+3)= -8-12=120

6(5-6)= (6 X 5)- (6 X4) = 30-24=6

FACTORIZACION

FACTORIZACION DE EXPRESIONES CON FUNCIÓN TRIGONOMÉTRICAS: Es posibles factorizar expresiones que involucran las funciones trigonométricas mediante lo mismo métodos de la factorizacion del polinomios

FACTOR COMÚN : En este caso es necesario identificar el factor que aparezca en todos los términos y aplicar la propiedad distributivas 

X (Y+Z)

X- Y +X Z

X (Y +Z)

FACTOR COMÚN POR AGRUPACIÓN 

En este casos se separan las expresiones en 2 o mas partes iguales (igual cantidad de terminos). en cada una de ella se identifica el factor común y se aplica la propiedad distributivas 

EJEMPLOS

1._(3cos³_{X + 6cos}²_{x) + (2cosx +4)}

(3.1 _cos²_{x+ 3.2 cos}²_{x)+ (2.1 cosx + 22)}

_3cos²_{x(1cosx + 2) + 2(1cosx +2)}

_{(1cosx +2) (3cos}²_x +2)

DIFERENCIAS DE CUADRADO

la diferencias de los cuadrados de 2 expresiones que involucran funciones trigonométricas es igual a la suma por la diferencia de las expresiones

TRINOMIO AL CUADRADO PERFECTO 

Un trinomio cuadrado perfecto, por brevedad TCP, es un polinomio de tres términos (también llamado trinomio) que resulta de elevar al cuadrado un binomio.

Todo trinomio de la forma:
${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}\,\!}$
es un trinomio cuadrado perfecto ya que
${\displaystyle (a+b)^{2}=(a+b)(a+b)=\,\!}$
${\displaystyle a^{2}+ab+ab+b^{2}=a^{2}+2ab+b^{2}\,\!}$

Siendo la regla: Cualquier suma de binomios al cuadrado es igual al cuadrado del primer término, más el doble del primer por el segundo término, más el cuadrado del segundo término. De lo anterior resulta que un trinomio será cuadrado perfecto siempre que se cumplan las siguientes condiciones:

1. El polinomio pueda ser ordenado en potencias descendentes de una variable.
2. Dos de los términos son cuadrados perfectos.
3. El otro término es el doble producto de las raíces cuadradas de los demás.
4. El primer y tercer término deben de tener el mismo signo

ÁNGULOS Y SISTEMAS DE MEDICIÓN

un angulo es una union de dos rayos o semirectas con el mismo origen, a las semirectas se les denomina lados y al origen comun se le llama vertice.

segun esta definicion el orden en que se nombran los lados de un angulo es diferente sin embargo en el estudio de la trigonometris es importante tener en cuenta el lado del angulo que se nombran primero ya que este nos da el sentido del angulo y apartir de hay se determina si es positivo o negativo considerados asi los angulos se lama orientados.

los angulos tambien se pueden detonar por las letras griegas

Α / α: Alfa

Β / β: Beta 

Θ / θ: theta

ANGULO SOBRE EL PLANO CARTESIANO

un angulo se considera en posicion canonica o normal cuando, en un sistema de cordenadas, el vertice de OC coincide con el origen y su lado inicial coiincide con el semieje positivo de x.

cuando un agulo se encuentra en posicion noormal, la ubicacion del lado final permite encontrar o determinar el cuadrante al cual pertenece. en los siguientes diagramas se presentan angulos en posicion normal ubicados en cada uno de los cuadrantes.

dos angulos en posicion normal pueden tener el mismo lado final en este caso se dicen que los angulos son coterminales. 

ANGULOS ESPECIALES

en algunos problemas de trigonometria es importante tener en cuenta los distinto tipos de angulos. los angulos se clasifican segun su medidas en:

ANGULO AGUDO: es el que mide menos de 90°

ANGULO RECTO: mide exactamente 90°

ANGULO OBTUSO: mides mas de 90° y menos de 180° grados

ANGULO LLANO: mide exactamente 80° grados 

segun la sumas de sus medidas los angulos pueden ser:

ANGULOS COMPLEMENTARIOS: cuando la sumas de sus medidas nos da 90° grados

ANGULOS SUPLEMENTARIOS: cuando la sumas de sus medidas es igual a 180| grados

MEDICIÓN DE ÁNGULOS

los angulos se miden en grados y en radianes. el grado es la unidad de medidas de los angulos en el sistema xesagesimal y el radial es la medidas de los angulos en el sistema ciclico.

MEDIDAS DE ANGULOS EN EL SISTEMA XESAGESIMAL

un angulo generado por la rotacion del lado final en una vuelta mide 360° grados. el grados xesagesimal(1°) se define como 1/360 de una vuelta.

un grado xesagesimal equivale a 60° grados.

EJEMPLOS

1. expresas el angulo 32,225° en grados, minutos y segundos.

32,225°= 32° 13´ 30"

32°

0,225 X 60 = 13,5

0,5 X 60 = 30

MEDIDAS DE ANGULOS EN EL SISTEMA CICLICO

sobre una circuferencia, un angulo central OC determina un arco AB. se dice que la medida de un angulo OC es un radial (1 Rad) si la longitud del arco AB que le corresponde es igual al radial de la circuferencia.

un radial es la medida de un angulos central de una circuferencia cuyo arco mide igual a un radio.

EQUIVALENCIAS ENTRE EL XESAGESIMAL EN EL SISTEMA CICLICO

puesto que la longitud de una circuferencia es igual a , se tiene que la longitud del arco corresponde a un angulo de 360° es igual a  arcos cuya medidas es R, por lo tanto 360° es igual a  radian.

para determinar la equivalencia de 1°en radianes se realiza los siguentes pasos:

360°=  rad 

180°= π rad = 1°X 180°= rad

1°= π rad/ 180

para determinar la equivalencia de un radian en grados se tienen que:

π rad = 180°

1 rad = 180°/π

en las siguentes figura se muestra algunas medidas en grados y radianes.

en los sistemas de medidas se puede expresar de grados a radianes y de radianes a grados.

TRIGONOMÉTRIA

la palabra trigonometria se deriva de 2 raizes griegas: trigos que significa triangulo y metra que significa medidas. la trigonometria se origino a bases como el estudio de las relaciones entre los lados y angulos de los triangulos y se empleo por resolver inicialmente problemas de navegacion y realizar calculos astronomicos 

DEFINICION DE LAS FUNCIONES TRIGONOMETRICAS DE UN ANGULO EN POSICION NORMAL

es un angulo en posicion normal y P( X,Y) es un punto cualquiera contenido al lado final diferente de 0 (0,0) se obtiene que :

P(X, Y)

0 (0,0)

0 P= Y =

para determinar el signo de las funciones trigonometrica debe considerarse el conportamiento de X de Y, R, si 

FUNCIONES PARA ANGULO CUADRANTALES

Hasta el momento se an estudiados los angulos cuyo lado final se encuentran en 1 de los 4 cuandrantes ahora es inportante considerar los angulos cuyo lado final coinciden con unos de los semiejes del plano cartesiano .

A los angulos en posicion normal cuyo lado final termina en algunos de los semiejes del plano cartesiano se le llaman angulos cuadrantes en la siguientes figura se representa los angulos cuadrantales . 90°,180°,270°,-90°,-180°-360°

RAZONES DE TRIGONOMETRICAS EN ANGULO RECTANGULO

Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo, asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos